

Next: The Peltier effect
Up: The origin of the
Previous: The origin of the
The experimental setup is shown schematically in
Fig. 1. The junctions 1 and 2 of the metallic wires made
of different materials 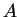 and
and 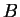 are kept at different
temperatures
are kept at different
temperatures 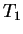 and
and 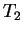 . The potential
. The potential 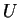 measured by the
voltmeter
measured by the
voltmeter 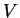 inserted into wire
inserted into wire 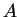 is given by
is given by
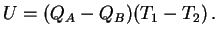 |
(1) |
Here 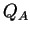 and
and 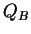 denote the Seebeck coefficient
(thermoelectric power) of metal
denote the Seebeck coefficient
(thermoelectric power) of metal 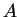 and
and 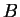 . The dimension of
. The dimension of 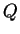 is energy/(charge
is energy/(charge 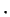 temperature). The natural unit of
thermopower is
temperature). The natural unit of
thermopower is
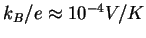 . Typical
. Typical 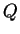 values for
metals are lower than that by a factor of 10 to 100, for
semiconductors they are higher by similar factors (see Figs. 2
and 3). If the temperature dependence of
values for
metals are lower than that by a factor of 10 to 100, for
semiconductors they are higher by similar factors (see Figs. 2
and 3). If the temperature dependence of 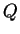 is taken into
account, eqn. (1) for the thermoelectric potental needs to
be replaced by a path integral, taken along the pieces of metal
between the exits
is taken into
account, eqn. (1) for the thermoelectric potental needs to
be replaced by a path integral, taken along the pieces of metal
between the exits 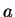 and
and 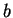 of the voltmeter in the circuit
shown in Fig. 1 (see Sec. 5, eqn. (12), below). However,
this modification is only of quantitative importance.
If the circuit of Fig. 1 is short-circuited by removing the
voltmeter, a stationary electric current flows. Approximately its
magnitude is given by the ratio of the thermoelectric potential
measured by the voltmeter and the total Ohmic resistance of the
circuit without voltmeter. While the thermoelectric potential is
low (in metals of order mV), this thermocurrent can be rather
large if the resistance is small.
of the voltmeter in the circuit
shown in Fig. 1 (see Sec. 5, eqn. (12), below). However,
this modification is only of quantitative importance.
If the circuit of Fig. 1 is short-circuited by removing the
voltmeter, a stationary electric current flows. Approximately its
magnitude is given by the ratio of the thermoelectric potential
measured by the voltmeter and the total Ohmic resistance of the
circuit without voltmeter. While the thermoelectric potential is
low (in metals of order mV), this thermocurrent can be rather
large if the resistance is small.
Figure 2:
The temperature dependence of the thermoelectric power
of some chosen metals (from [2])
|
|
Figure 3:
The temperature dependence of the thermoelectric power
of silicon containing different kinds of impurity (from [2]).
|
|


Next: The Peltier effect
Up: The origin of the
Previous: The origin of the
Klaus Froboese
2000-11-07