

Next: Currents of diffusing particles:
Up: The origin of the
Previous: Thermoelectric potential and contact
Thermopower und thermodiffusion
In the presence of a temperature gradient in a conductor
a second contribution to the electric current due to
thermodiffusion occurs in addition to the current given by Ohm's
law. Under conditions of zero electric current the two current
contributions must compensate each other. Since the Ohmic current
is proportional to a potential difference and the thermodiffusion
current is proportional to a temperature difference, a
proportionality between potential and temperature difference
results, which corresponds to eqn. (1). This is explained in
detail in the following.
We first note that the difference (10) of the
electrochemical potential as measured in the voltmeter can
be expressed as a path integral of its gradient along the three
portions of metal between the exits 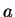 and
and 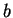 (see Fig. 1):
(see Fig. 1):
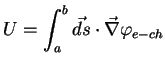 |
(11) |
Since, according to (7), the electrochemical potential is
continuous at the junctions of the two metals, there is no
contribution to (11) from the junctions. On the other hand,
the thermoelectric potential is given by the exact expression
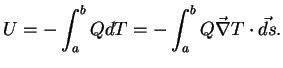 |
(12) |
In case the Seebeck coefficients of both metals are independent
of temperature eqn. (12) reduces to the eqn. (1).
Comparing the path integrals (11) and (12) we find the
equation
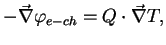 |
(13) |
which is the local form of the law for the thermoelectric
potential. It is now shown that the relation (13) results
from the thermodiffusion of the conduction electrons. This holds
both for metals and semiconductors.
Subsections


Next: Currents of diffusing particles:
Up: The origin of the
Previous: Thermoelectric potential and contact
Klaus Froboese
2000-11-07
![]() and
and ![]() (see Fig. 1):
(see Fig. 1):