


Nächste Seite: Berechnung des Thermodiffusionsstroms
Aufwärts: Thermokraft und Thermodiffusion
Vorherige Seite: Thermokraft und Thermodiffusion
Diffusionsvorgänge sind immer Ausgleichsvorgänge. Der Diffusionsstrom
von Teilchen ist so gerichtet, daß er eine vorhandene Inhomogenität
der Teilchendichte 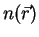 ausgleicht.
Dies wird durch das Ficksche Gesetz
für die Diffusionsstromdichte
ausgleicht.
Dies wird durch das Ficksche Gesetz
für die Diffusionsstromdichte
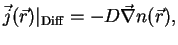 |
(14) |
in dem 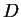 den Diffusionskoeffizienten darstellt, ausgedrückt. Ein
Wärmestrom zielt dagegen auf den Ausgleich der Temperatur.
Dem entspricht das Fouriersche Gesetz
den Diffusionskoeffizienten darstellt, ausgedrückt. Ein
Wärmestrom zielt dagegen auf den Ausgleich der Temperatur.
Dem entspricht das Fouriersche Gesetz
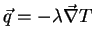 |
(15) |
für die Wärmestromdichte 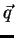 , in dem
, in dem 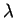 die
Wärmeleitfähigkeit bezeichnet. In diesem einfachen Bild von
Diffusionsvorgängen kommt die
Thermodiffusion aber nicht vor!
die
Wärmeleitfähigkeit bezeichnet. In diesem einfachen Bild von
Diffusionsvorgängen kommt die
Thermodiffusion aber nicht vor!
Die anschaulich verständlichen Ausdrücke (14) und (15) sind
nicht vollständig: Ersterer gilt nur bei konstanter Temperatur, letzterer nur
bei konstanter Dichte. Zusätzlich gibt es ``Kreuzterme'', proportional zu
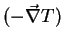 zur Teilchenstromdichte und proportional zu
zur Teilchenstromdichte und proportional zu
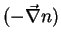 zur Wärmestromdichte. Der Beitrag des Temperaturgradienten
zur Wärmestromdichte. Der Beitrag des Temperaturgradienten
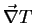 zur Teilchenstromdichte beschreibt die Thermodiffusion. Der Ausdruck
für die Stromdichte dieses Thermodiffusionsstroms wird im
folgenden Abschnitt abgeleitet (Gl. (24)). (Mathematisch
gesprochen stellen der Diffusionskoeffizient
zur Teilchenstromdichte beschreibt die Thermodiffusion. Der Ausdruck
für die Stromdichte dieses Thermodiffusionsstroms wird im
folgenden Abschnitt abgeleitet (Gl. (24)). (Mathematisch
gesprochen stellen der Diffusionskoeffizient 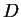 in (14) und die
Wärmeleitfähigkeit
in (14) und die
Wärmeleitfähigkeit 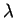 in (15) nur die Diagonalelemente einer
in (15) nur die Diagonalelemente einer
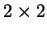 Matrix von Koeffizienten in den allgemeinen Ausdrücken für
Matrix von Koeffizienten in den allgemeinen Ausdrücken für 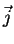 und
und 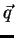 bei gegebenem Dichte- und Temperaturgradient dar. Dazu kommen
zwei Außerdiagonalelemente der Koeffizientenmatrix, welche die ``Kreuzterme''
in den Ausdrücken für
bei gegebenem Dichte- und Temperaturgradient dar. Dazu kommen
zwei Außerdiagonalelemente der Koeffizientenmatrix, welche die ``Kreuzterme''
in den Ausdrücken für 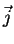 und
und 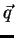 liefern. Daß diese Kreuzterme
nicht ebenso unmittelbar plausibel gemacht werden können wie die Hauptterme
(14) und (15), zeigt sich auch darin, daß ihre Koeffizienten
nicht wie
liefern. Daß diese Kreuzterme
nicht ebenso unmittelbar plausibel gemacht werden können wie die Hauptterme
(14) und (15), zeigt sich auch darin, daß ihre Koeffizienten
nicht wie 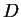 und
und 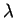 immer positiv sind.)
immer positiv sind.)
Leider gilt die oben gegebene Darstellung des Ausgleichs von
Dichteinhomogenitäten durch Diffusion (Gl. (14)) nur für ungeladene diffundierende
Teilchen.
Für Ladungsträger ist sie unvollständig!
Eine Anhäufung von gleichnamig geladenen Teilchen erzeugt
nämlich ein elektrisches Feld, welches die Ladungen
zusätzlich zum Diffusionsvorgang auseinandertreibt.
Für die Stromdichte eines solchen durch ein elektrisches Feld
angetriebenen ``Driftstroms'' gilt der Ausdruck
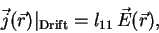 |
(16) |
worin 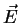 die elektrische Feldstärke ist und der Transportkoeffizient
die elektrische Feldstärke ist und der Transportkoeffizient 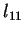 über die Beziehung
über die Beziehung
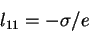 |
(17) |
mit der spezifischen Leitfähigkeit 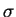 zusammenhängt. Man kann zeigen (siehe z. B. [4]), daß die
Gesamtstromdichte aus Diffusions- und Driftstrom durch den Ausdruck
zusammenhängt. Man kann zeigen (siehe z. B. [4]), daß die
Gesamtstromdichte aus Diffusions- und Driftstrom durch den Ausdruck
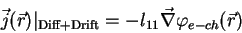 |
(18) |
gegeben ist, den man erhält, wenn man in Gl.(16) den Gradienten des elektrischen
Potentials durch jenen des elektrochemischen Potentials (8) ersetzt.



Nächste Seite: Berechnung des Thermodiffusionsstroms
Aufwärts: Thermokraft und Thermodiffusion
Vorherige Seite: Thermokraft und Thermodiffusion
Klaus Froböse
4. Juni 1999
![]() zur Teilchenstromdichte und proportional zu
zur Teilchenstromdichte und proportional zu
![]() zur Wärmestromdichte. Der Beitrag des Temperaturgradienten
zur Wärmestromdichte. Der Beitrag des Temperaturgradienten
![]() zur Teilchenstromdichte beschreibt die Thermodiffusion. Der Ausdruck
für die Stromdichte dieses Thermodiffusionsstroms wird im
folgenden Abschnitt abgeleitet (Gl. (24)). (Mathematisch
gesprochen stellen der Diffusionskoeffizient
zur Teilchenstromdichte beschreibt die Thermodiffusion. Der Ausdruck
für die Stromdichte dieses Thermodiffusionsstroms wird im
folgenden Abschnitt abgeleitet (Gl. (24)). (Mathematisch
gesprochen stellen der Diffusionskoeffizient ![]() in (14) und die
Wärmeleitfähigkeit
in (14) und die
Wärmeleitfähigkeit ![]() in (15) nur die Diagonalelemente einer
in (15) nur die Diagonalelemente einer
![]() Matrix von Koeffizienten in den allgemeinen Ausdrücken für
Matrix von Koeffizienten in den allgemeinen Ausdrücken für ![]() und
und ![]() bei gegebenem Dichte- und Temperaturgradient dar. Dazu kommen
zwei Außerdiagonalelemente der Koeffizientenmatrix, welche die ``Kreuzterme''
in den Ausdrücken für
bei gegebenem Dichte- und Temperaturgradient dar. Dazu kommen
zwei Außerdiagonalelemente der Koeffizientenmatrix, welche die ``Kreuzterme''
in den Ausdrücken für ![]() und
und ![]() liefern. Daß diese Kreuzterme
nicht ebenso unmittelbar plausibel gemacht werden können wie die Hauptterme
(14) und (15), zeigt sich auch darin, daß ihre Koeffizienten
nicht wie
liefern. Daß diese Kreuzterme
nicht ebenso unmittelbar plausibel gemacht werden können wie die Hauptterme
(14) und (15), zeigt sich auch darin, daß ihre Koeffizienten
nicht wie ![]() und
und ![]() immer positiv sind.)
immer positiv sind.)