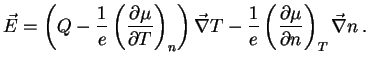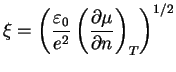Nächste Seite: Nichtstationäre Bedingungen
Aufwärts: Wo sitzen die elektrischen
Vorherige Seite: Wo sitzen die elektrischen
Wir zeigen, daß sich im Inneren der beiden
Leiter 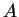 und
und 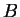 keine Ladungen befinden. Mit (8) und (28)
erhalten wir aus
(26) und (27) für die elektrische Feldstärke
keine Ladungen befinden. Mit (8) und (28)
erhalten wir aus
(26) und (27) für die elektrische Feldstärke
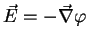
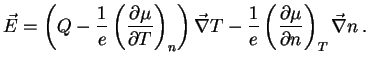 |
(31) |
Den Koeffizienten von
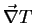 auf der rechten Seite
bezeichnen wir mit
auf der rechten Seite
bezeichnen wir mit
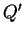 . Bilden wir die Divergenz des Ausdrucks (31), wobei wir
eine von einer Temperaturabhängigkeit herrührende räumliche
Veränderlichkeit des Koeffizienten
. Bilden wir die Divergenz des Ausdrucks (31), wobei wir
eine von einer Temperaturabhängigkeit herrührende räumliche
Veränderlichkeit des Koeffizienten 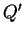 und der Ableitung
und der Ableitung
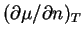 vernachlässigen, so erhalten wir
vermöge der Maxwellgleichung
vernachlässigen, so erhalten wir
vermöge der Maxwellgleichung
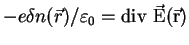 |
(32) |
für die Ladungsdichte
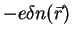 die Gleichung
die Gleichung
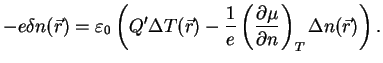 |
(33) |
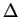 bezeichnet den Laplaceoperator. Da aus der Wärmeleitungsgleichung
bezeichnet den Laplaceoperator. Da aus der Wärmeleitungsgleichung
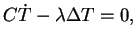 |
(34) |
worin 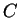 die spezifische Wärme pro Volumen angibt, im angenommenen
stationären Fall folgt
die spezifische Wärme pro Volumen angibt, im angenommenen
stationären Fall folgt
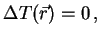 |
(35) |
reduziert sich die Gleichung (33) für die Ladungsdichte auf
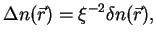 |
(36) |
worin
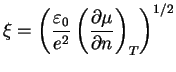 |
(37) |
eine Länge von atomarer Größenordnung bezeichnet. Die
Lösung der Differentialgleichung (36) fällt ins Innere der Leiter
im Maßstab dieser Länge 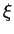 exponentiell auf null ab.
(Es sei auf folgende Analogie aufmerksam gemacht: In der
Londonschen Theorie der Supraleitung folgt aus der
mathematisch mit (36) äquivalenten Gleichung für die
magnetische Induktion
exponentiell auf null ab.
(Es sei auf folgende Analogie aufmerksam gemacht: In der
Londonschen Theorie der Supraleitung folgt aus der
mathematisch mit (36) äquivalenten Gleichung für die
magnetische Induktion 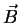 die Verdrängung des
die Verdrängung des 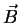 -Feldes
aus dem Innern eines Supraleiters (Meißner-Ochsenfeld-Effekt) [4].)
-Feldes
aus dem Innern eines Supraleiters (Meißner-Ochsenfeld-Effekt) [4].)
Im makroskopischen Längenmaßstab gilt somit im Leiterinneren
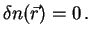 |
(38) |
Die gesuchten Ladungen können also nur auf den
Grenzflächen an den Leiterkontakten
und den Leiteroberflächen sitzen!



Nächste Seite: Nichtstationäre Bedingungen
Aufwärts: Wo sitzen die elektrischen
Vorherige Seite: Wo sitzen die elektrischen
Klaus Froböse
4. Juni 1999