

Next: Proof of charge neutrality
Up: The origin of the
Previous: Compensation of the thermodiffusion
As we have seen that the thermoelectric potential
measured in a thermoelectric circuit is of purely electrostatic
origin, we ask by which electric charges this potential is
generated.
As is shown below, inside a homogeneous conductor charge
neutrality is maintained even in the presence of a stationary
temperature gradient. Therefore the electric charges generating
the thermoelectric potential can only sit at the surface of the
conductor, including the interface at the junctions with another
conducting material.
The distribution of these charges can be inferred from the
variation of the electrostatic potential (Fig. 10).
The electrostatic potential follows via
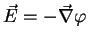 |
(28) |
from the result (31) derived below as
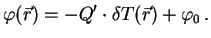 |
(29) |
Here the coefficients 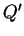 and the constants of integration
and the constants of integration
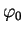 are different for the two conductors. The potential
are different for the two conductors. The potential
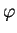 must fulfil the condition of continuity (7) at the
interfaces. This potential pattern is explained qualitatively by
a charge distribution as drawn in Fig. 11 (assuming
must fulfil the condition of continuity (7) at the
interfaces. This potential pattern is explained qualitatively by
a charge distribution as drawn in Fig. 11 (assuming
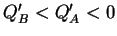 ). At the interfaces a positive or
negative charge cloud is superimposed on the electric double
layer. Charges are also located at the surfaces of the
conductors, especially near the points of contact.
). At the interfaces a positive or
negative charge cloud is superimposed on the electric double
layer. Charges are also located at the surfaces of the
conductors, especially near the points of contact.
Figure 11:
Distribution of electric charge at the surfaces and
interfaces of a thermoelectric circuit (schematic).
|
|
The magnitude of the total electric charge generating the
thermoelectric potential, according to Fig. 12, can be
estimated as
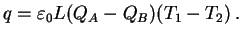 |
(30) |
For
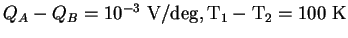 and
and
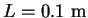 one obtains
one obtains
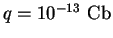 as
an order of magnitude. This is a very small charge indeed,
amounting to about
as
an order of magnitude. This is a very small charge indeed,
amounting to about 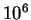 electron charges. To my knowledge, so
far the electric (and upon rotation: magnetic) field generated by
this charge has not been measured directly outside the conductors.
electron charges. To my knowledge, so
far the electric (and upon rotation: magnetic) field generated by
this charge has not been measured directly outside the conductors.
Figure 12:
Estimate of total electric charge in a thermoelectric
circuit.
|
|
Subsections


Next: Proof of charge neutrality
Up: The origin of the
Previous: Compensation of the thermodiffusion
Klaus Froboese
2000-11-07