
Next: Compensation of the thermodiffusion
Up: Thermopower und thermodiffusion
Previous: Currents of diffusing particles:
We imagine that an electron at position 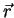 has been
scattered last at a distance given by the mean free path
has been
scattered last at a distance given by the mean free path 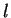 , and
we make the simplifying assumption that in this event the
electron has assumed a velocity of absolute magnitude given by
the mean value
, and
we make the simplifying assumption that in this event the
electron has assumed a velocity of absolute magnitude given by
the mean value
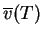 which corresponds to the local
temperature
which corresponds to the local
temperature 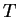 . It follows that an electron at
. It follows that an electron at 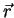 with
direction of flight
with
direction of flight 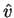 has a velocity given by
has a velocity given by
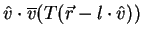 (Fig. 9). Averaging over the direction
(Fig. 9). Averaging over the direction 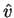 , one
obtains
for the mean electronic velocity
, one
obtains
for the mean electronic velocity
Expanding
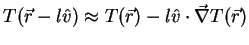 |
(20) |
and
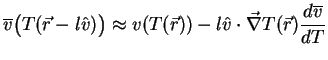 |
(21) |
one arrives at
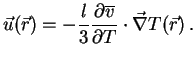 |
(22) |
According to this result the different speeds, corresponding to
different kinetic energies, of electrons arrived from different
directions lead to a mean velocity in a direction opposite to the
temperature gradient. This is the phenomenon of thermodiffusion!
With (22) one obtains the corresponding current density as
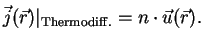 |
(23) |
Introducing an off-diagonal transport coefficient 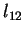 this
result can be written as
this
result can be written as
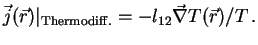 |
(24) |
Comparison of (24) with (22) and (23)
yields for 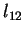
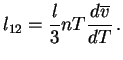 |
(25) |
Figure 9:
Calculation of the current of thermodiffusion.
|
|


Next: Compensation of the thermodiffusion
Up: Thermopower und thermodiffusion
Previous: Currents of diffusing particles:
Klaus Froboese
2000-11-07