
Next: Non-stationary conditions
Up: Where do the electric
Previous: Where do the electric
We show that no charges exist inside the conductors  and
and 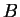 .
With (8) and (28) we obtain from (26) and
(27) for the electric field
.
With (8) and (28) we obtain from (26) and
(27) for the electric field
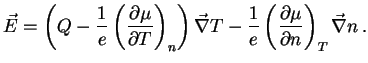 |
(31) |
We denote the coefficient of
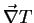 on the r.h.s. by
on the r.h.s. by
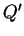 . Taking the divergence and neglecting a spatial
variation of this coefficient and of the derivative
. Taking the divergence and neglecting a spatial
variation of this coefficient and of the derivative
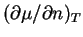 , which may result from the
temperature variation, we obtain, using the Maxwell equation
, which may result from the
temperature variation, we obtain, using the Maxwell equation
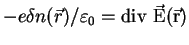 |
(32) |
the following equation for the charge density
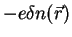 :
:
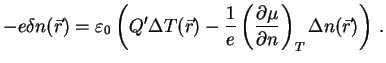 |
(33) |
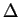 stands for the Laplacian. Under stationary conditions as
assumed the heat conduction equation
stands for the Laplacian. Under stationary conditions as
assumed the heat conduction equation
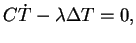 |
(34) |
where 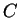 denotes the specific heat per volume, leads to
denotes the specific heat per volume, leads to
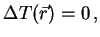 |
(35) |
which reduces eqn. (33) to the homogeneous differential
equation
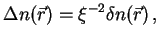 |
(36) |
where
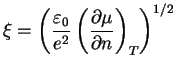 |
(37) |
is a screening length of atomic dimension. Inside a conductor the
solution of eqn. (36) decays to zero exponentially within a
distance from the surface given by  . (We note the following
analogy: In the London theory of supraconductivity an equation of
the same form as eqn. (36) describes the expulsion of the
magnetic field from the interior of a superconductor
(Meissner-Ochsenfeld effect) [3].) On a macroscopic scale,
therefore, the condition of charge neutrality
. (We note the following
analogy: In the London theory of supraconductivity an equation of
the same form as eqn. (36) describes the expulsion of the
magnetic field from the interior of a superconductor
(Meissner-Ochsenfeld effect) [3].) On a macroscopic scale,
therefore, the condition of charge neutrality
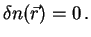 |
(38) |
holds. The charges generating the thermoelectric potential must be
located exclusively at surfaces and interfaces!


Next: Non-stationary conditions
Up: Where do the electric
Previous: Where do the electric
Klaus Froboese
2000-11-07